Counting: Geometrical Patterns
@ : Home >
Geometrical Patterns >
Shortcuts with Examples
Counting: Shortcuts with Examples
|
Questions from this topic involve counting of geometrical figures such as squares, rectangles, triangles,
parallelogram, quadrilaterals etc. in a given figure. We must count figures in a systematic method to save
time. If we count the figures randomly, then we may make a mistake. So avoid counting figures randomly. Let us consider some of the standard patterns and methods for counting the geometrical figures. Consider a 4×4 square. Total number of squares formed can be counted as discussed below.  Number of 1 × 1 squares: 16 = 42
Number of 1 × 1 squares: 16 = 42Number of 2 × 2 squares: 9 = 32 Number of 3 × 3 squares: 4 = 22 Number of 4 × 4 squares: 1 = 12 Total number of squares = 12 + 22 + 32 + 42 = (1 + 4 + 9 + 16) = 30 The formula can be generalized as under: For a n×n square. Total number of squares formed are = 12 + 22 + 32 + .... + n2 = n(n + 1)(2n + 1)/6. Example: For a 6×6 square n = 6 Total number of squares formed = 6(6 + 1)(2×6 + 1)/6 = 91 Example: Find the total number of squares in the adjacent figure. 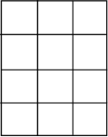 Given figure is a rectangle of size 3 × 4. The smaller side is subdivided into 3 equal parts and the bigger side is subdivided into 4 equal parts, 12 smaller squares of equal size are obtained. Now, the total number of squares in the figure can be counted as explained below: Number of 1 × 1 squares = 3 × 4 = 12 Number of 2 × 2 squares = 2 × 3 = 6 Number of 3 × 3 squares = 1 × 2 = 2 Total number of squares formed = (3 × 4) + (2 × 3) + (1 × 2) = 12 + 6 + 2 = 20. Similarly, if a rectangle is of size 4 × 5 the total number of squares formed = (4 × 5) + (3 × 4) + (2 × 3) + (1 × 2) = 20 + 12 + 6 + 2 = 40 Similarly, if a rectangle is of size 5 × 6 the total number of squares formed = (5 × 6) + (4 × 5) + (3 × 4) + (2 × 3) + (1 × 2) = 30 + 20 + 12 + 6 + 2 = 70 For a rectangle of dimension m × n the formula can be generalised as under The total number of squares formed is equal to (m)×(n) + (m – 1)×(n – 1) + ... until one of the terms becomes zero. |