L.C.M and H.C.F.
@ : Home >
LCM and HCF >
Important Tricks and Formulas
Important Tricks and Formulas for LCM and HCF
L.C.M. (Least Common Multiple)L.C.M. of two or more numbers is the smallest number which is exactly divisible by each of the numbers.Methods to find L.C.M.: 1) Factorization method: Express each of the numbers as the product of prime numbers. L.C.M. is the product of highest powers of the prime numbers.Example: L.C.M. of 2x2y3z7 and 3xy4z3 is 6x2y4z7 where x,y,z are the prime factors. H.C.F. (Highest Common Factor) or G.C.D. (Greatest Common Divisor)H.C.F. of two or more numbers is the greatest number which is present in each of the numbers.Methods to find H.C.F.: 1) Factorization method to find H.C.F.: Express each of the numbers as the product of prime numbers. H.C.F. is the product of least powers of the common prime numbers.Example: H.C.F. of 2x2y3z7 and 3xy4z3 is xy3z3 where x,y,z are the prime factors. Finding H.C.F. of more than two numbers:Suppose there are three numbers a, b, cFind the H.C.F. of a, b. Suppose H.C.F.(a, b) = h1 Now find H.C.F. of (h1, c). Suppose H.C.F.(h1, c) = h2 So, we can say that the H.C.F.(a, b, c) = h2 Finding L.C.M. and H.C.F. of fractions:L.C.M. of fractions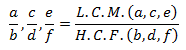 H.C.F. of fractions 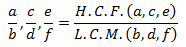 NOTE: 1) All the fractions of 2 or more must be in their lowest terms. If they are not in their lowest terms, then conversion in the lowest form is required before finding the HCF or LCM. 2) The required HCF of 2 or more fractions is the highest fraction which exactly divides each of the fractions. H.C.F of coprime numbers is 1. 3) The required LCM of 2 or more fractions is the least fraction/integer which is exactly divisible by each of them. 4) The HCF of numbers of fractions is always a fraction but this is not true in case of LCM. H.C.F. × L.C.M. = Product of numbers. (This formula is applicable only for 2 numbers.) The greatest number which divides the numbers x, y and z leaving remainders a, b and c respectively is given by HCF of (x - a), (y - b) and (z - c). Example: Find the greatest number which divides 29, 60 and 103 leaving remainders 5, 12 and 7 respectively. Solution:x = 29, y = 60, z = 103 a = 5, b = 12, c = 7. Required number is HCF of (29 - 5), (60 - 12), (103 - 7) = HCF of 24, 48, 96 = 24. The least number which when divided by x, y and z leaves the remainders a, b and c respectively is given by (LCM of x,y,z) - k where k = x - a = y - b = z - c. Example: Find the least number which when divided by 24, 32 and 36 leaves the remainders 19, 27 and 31 respectively. Solution: x = 24, y = 32, z = 36, a = 19, b = 27, c = 31. k = 24 - 19 = 32 - 27 = 36 - 31 = 5. Required number is (LCM of 24, 32, 36) - 5 = 288 - 5 = 283. |