Counting
Q1) What is the minimum number of colours required to fill the spaces in the given diagram without any two
adjacent spaces having the same colour?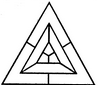 1) 3 2) 4 3) 5 4) 6 Solution: The figure may be labelled as shown. 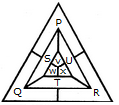 The spaces P, Q and R have to be shaded by three different colours definitely (since each of these three spaces lies adjacent to the other two). Now, in order that no two adjacent spaces be shaded by the same colour, the spaces T, U and S must be shaded with the colours of the spaces P, Q and R respectively. Also the spaces X, V and W must be shaded with the colours of the spaces S, T and U respectively i.e. with the colours of the spaces R, P and Q respectively. Thus, minimum three colours are required. Q2) What is the minimum number of different colours required to paint he given figure such that no two adjacent regions have the same colour? 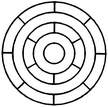 1) 3 2) 4 3) 5 4) 6 Solution: The figure may be labelled as shown. 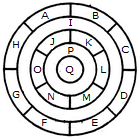 The regions A, C, E and G can have the same colour say colour 1. The regions B, D, F and H can have the same colour (but different from colour 1) say colour 2. The region 1 lies adjacent to each one of the regions A, B, C, D, E, F, G and H and therefore it should have a different colour say colour 3. The regions J, L and N can have the same colour (different from colour 3) say colour 1. The regions K, M and O can have the same colour (different fromthe colours 1 and 3). Thus, these regions will have colour 2. The region P cannot have any of the colours 1 and 2 as it lies adjacent to each one of the regions J, K, L, M, N and O and so it will have colour 3. The region Q can have any of the colours 1 or 2. Minimum number of colours required is 3. Read More: Questions on Counting number of TrianglesDownload: Practice Questions on Counting Geometrical FiguresQ3) In the adjoining figure, if the centres of all the circles are joined by horizontal and vertical lines, then find the number of squares that can be formed. 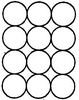 1) 1 2) 6 3) 7 4) 8 Solution: The figure may be labelled as shown. 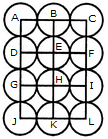 We shall join the centres of all the circles by horizontal and vertical lines and then label the resulting figure as shown. The simplest squares are ABED, BCFE, DEHG, EFIH, GHKJ and HILK i.e. 6 in number. The squares composed of four simple squares are ACIG and DFLJ i.e. 2 in number. Thus, 6 + 2 = 8 squares will be formed. Q4) Count the number of convex pentagons in the adjoining figure. 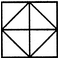 1) 4 2) 8 3) 12 4) 16 Solution: A convex pentagon has no angles pointing inwards. More precisely, no internal angles can be more than 180°. The figure may be labelled as shown. 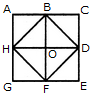 The pentagons in the figure, are ABDFH, CDFHB, EFHBD, GHBDF, ACDFG, CEFHA, EGHBC, GABDE, BDEGH, DFGAB, FHACD and HBCEF. Clearly, these are 12 in number. Read More: Questions on Counting number of RectanglesRead More: Shortcuts for Geometrical PatternsQ5) What is the minimum number of straight lines that is needed to construct the figure?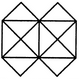 1) 11 2) 13 3) 15 4) 21 Solution: The figure may be labelled as shown. 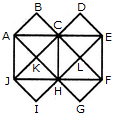 The horizontal lines are AE and JF i.e. 2 in number. The vertical lines are AJ, CH and EF i.e. 3 in number. The slanting lines are AG, BF, JD, IE, AB, DE, JI and FG i.e. 8 in number. Total number of straight lines needed to construct the figure = 2 + 3 + 8 = 13. Q6) How many circles are there in the adjoining figure. 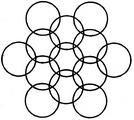 1) 11 2) 12 3) 13 4) 14 Solution: The figure may be labelled as shown. 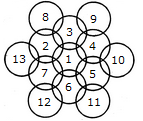 There are 13 circles in the given figure. This is clear from the adjoining figure in which the centres of all the circles in the given figure have been numbered from 1 to 13. Read More: Questions on Counting number of Parallelograms |