Counting
Counting Squares
Q1) Count the number of squares in the given figure 1) 28 2) 29 3) 30 4) 32 Solution: The figure may be labelled as shown. 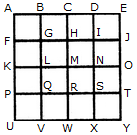 The simplest squares are ABGF, BCHG, CDIH, DEJI, FGLK, GHML, HINM, IJON, KLQP, LMRQ, MNSR, NOTS, PQVU, QRWV, RSXW and STYX i.e. 16 in number. The squares composed of four components each are ACMK, BDNL, CEOM, FHRP, GISQ, HJTR, KMWU, LNXV and MOYW i.e. 9 in number. The squares composed of nine components each are ADSP, BETQ, FIXU and GJYV i.e. 4 in number. There is one square AEYU composed of sixteen components. There are 16 + 9 + 4 + 1 = 30 squares in the given figure. Q2) Count the number of squares in the given figure 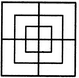 1) 8 2) 12 3) 15 4) 18 Solution: The figure may be labelled as shown. 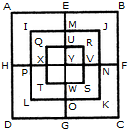 The simplest squares are QUYX, URVY, YVSW and XYWT i.e. 4 in number. The squares composed of two components each are IMYP, MJNY, YNKO and PYOL i.e. 4 in number. The squares composed of three components each are AEYH, EBFY, YFCG and HYGD i.e. 4 in number. There is only one square i.e. QRST composed of four components. There is only one square i.e. IJKL composed of eight components. There is only one square i.e. ABCD composed of twelve components. Total number of squares in the given figure = 4 + 4 + 4 + 1 + 1 + 1 = 15. Read More: Questions on Counting number of TrianglesDownload: Practice Questions on Counting Geometrical FiguresQ3) Count the number of squares in the given figure 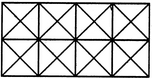 1) 11 2) 21 3) 24 4) 26 Solution: The figure may be labelled as shown. 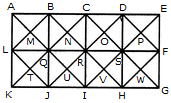 The squares composed of two components each are BNQM, CORN, DPSO, MQTL, NRUQ, OSVR, PFWS, QUJT, RVIU and SWHV i.e. 10 in number. The squares composed of four components each are ABQL, BCRQ, CDSR, DEFS, LQJK, QRIJ, RSHI and SFGH i.e. 8 in number. The squares composed of eight components each are BRJL, CSIQ and DFHR i.e. 3 in number. The squares composed of sixteen components each are ACIK, BDHJ and CEGI i.e. 3 in number. Thus, there are 10 + 8 + 3 + 3 = 24 squares in the figure. Q4) Count the number of squares in the given figure 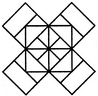 1) 14 2) 18 3) 20 4) 22 Solution: The figure may be labelled as shown. 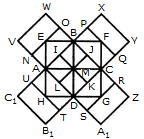 The squares composed of two components each are BJMI, CKMJ, DLMK and AIML i.e. 4 in number. The squares composed of three components each are EBMA, BFCM, MCGD and AMDH i.e. 4 in number. The squares composed of four components each are VWBA, XYCB, ZA1DC and B1C1AD i.e. 4 in number. The squares composed of seven components each are NOJL, PQKI, RSLJ and TUIK i.e. 4 in number. There is only one square i.e. ABCD composed of eight components. There is only one square i.e. EFGH composed of twelve components. Total number of squares in the figure = 4 + 4 + 4 + 4 + 1 + 1 = 18. Read More: Questions on Counting number of RectanglesRead More: Shortcuts for Geometrical PatternsQ5) Count the number of squares in the given figure 1) 18 2) 19 3) 25 4) 27 Solution: The figure may be labelled as shown. 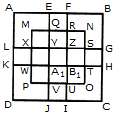 The simplest squares are EFRQ, MQYX, QRZY, RNSZ, LXWK, XYA1W, YZB1A1, ZSTB1, SGHT, WA1VP, A1B1UV, B1TOU and VUIJ i.e. 13 in number. The squares having two components each are AEYL, FBGZ, KA1JD and B1HCI i.e. 4 in number. The squares having four components each are MRB1W, QNTA1, XZUP and YSOV i.e. 4 in number. The squares having seven components each are AFB1K, EBHA1 LZID and YGCJ i.e. 4 in number. There is only one square i.e. MNOP composed of nine components. There is only one square i.e. ABCD composed of seventeen components. There are 13 + 4 + 4 + 4 + 1 + 1 = 27 squares in the figure. Q6) Count the number of squares in the given figure 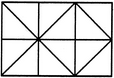 1) 6 2) 7 3) 9 4) 10 Solution: The figure may be labelled as shown. 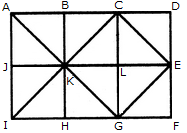 The squares composed of two components each are ABKJ, BCLK, CDEL, LEFG, KLGH and JKHI i.e.6 in number. There is only one square i.e. CEGK composed of four components. The squares composed of eight components each are ACGI and BDFH i.e. 2 in number. There are 6 + 1 + 2 = 9 squares in the figure. Read More: Questions on Counting number of Parallelograms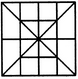 1) 13 2) 16 3) 19 4) 20 Solution: The figure may be labelled as shown. 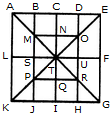 The simplest squares are BCNM, CDON, PQIJ and QRHI i.e. 4 in number. The squares composed of two components each are MNTS, NOUT, STQP and TURQ i.e. 4 in number. The squares composed of five components each are ACTL, CEFT, TFGI and LTIK i.e. 4 in number. The squares composed of six components each are BDUS and SUHJ i.e. 2 in number. There is only one square i.e. MORP composed of eight components. There is only one square i.e. AEGK composed of twenty components. Total number of squares in the figure = 4 + 4 + 4 + 2 + 1 + 1 = 16. |